According to the PDF file that Ma'am Jing sent us:
We can estimate the shape of the surface by capturing multiple images of the surface with the sources at different locations. The information about the surface will be coded in the shadings obtained from the images.
If there are N images in 3D space. We can define a matrix
where each row is a source, each column is the x,y,z component of the source. If we take N images of the surface using each of these N sources, then for each point (x,y) on the surface we have

Since I and V are already given we could compute for the matrix g by using the equation given below.
Then we get the normal vector by the equation below.

Then we get the normal vector by the equation below.

We can now calculate the shape of the object using the following equations.
We were given the matrix V.
V1 = {0.085832, 0.17365, 0.98106}
V2 = {0.085832, -0.17365, 0.98106}
V3 = {0.17365, 0, 0.98481}
V4 = {0.16318, -0.34202, 0.92542}
The data within the matlab file contains the intensity of the four images the intensities are in 128*128 matrices. We reshape these matrices into a row matrices in order to obtain the matrix I. Then when we finally get df/dx and df/dy by using the normal vector we reshape these back to a 128*128 matrices for us to reconstruct the 3D object. The four images below are the ones used in the activity. The following image is the reconstructed 3D object.

V1 = {0.085832, 0.17365, 0.98106}
V2 = {0.085832, -0.17365, 0.98106}
V3 = {0.17365, 0, 0.98481}
V4 = {0.16318, -0.34202, 0.92542}
The data within the matlab file contains the intensity of the four images the intensities are in 128*128 matrices. We reshape these matrices into a row matrices in order to obtain the matrix I. Then when we finally get df/dx and df/dy by using the normal vector we reshape these back to a 128*128 matrices for us to reconstruct the 3D object. The four images below are the ones used in the activity. The following image is the reconstructed 3D object.

We see that the reconstructed 3D image is a sphere with a cross structure. This 3D image is similar to the 4 2D images which means that our reconstruction was successful.
I give myself a grade of 10 for successfully doing the activity.
Thank you for Rafael Jaculbia, Jorge Presto and Billy Narag for helping me in this activity. Also thanks to Cole and Jeric.
I give myself a grade of 10 for successfully doing the activity.
Thank you for Rafael Jaculbia, Jorge Presto and Billy Narag for helping me in this activity. Also thanks to Cole and Jeric.

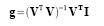





No comments:
Post a Comment