
Max grayscale pixel value = 103
Min grayscale pixel value = 17
Above is the histogram of the original image. We can see that it has only a limited range of grayscale values which means the image is of poor contrast.
The Cumulative Distribution Function (CDF) is shown above. The CDF is not linear and has a point of saturation where the value becomes 1 which is the highest value of the CDF
We backproject the image pixel values by finding its corresponding y-value in the CDF. That is, replace the pixel value by the values on the y-axis of the pixel value from the CDF. The resulting image is called the histogram equalized image. The histogram equalized image is shown below.
We could see visually that the contrast was improved. We verify this by looking at its histogram. The histogram is shown below.
The histogram is well spread which means that the image has good contrast. Comparing it to the original image, the contrast of the histogram equalized image is far much better. The CDf is shown below and it can be seen that it is linear.
I used another method to improve the contrast of my image. I stretched my CDF and in the process also stretched the range of grayscale values that are present. The resulting image, its histogram and CDF is shown below.
At the last part of the activity we transformed the image to have a desired CDF. The desired CDF equation has the equation G=tanh(16*(z-128)/255). But since the values must be from zero to one then we normalize the equation by adding one then dividing it by the maximum value. I did that on scilab and I get the CDF below.
Now we use the algorithm
1. From the pixel grayscale, find CDF value.
2.Trace this value in the desired CDF.
3.Replace pixel value by grayscale value having this CDF value in desired CDF.
The resulting image is shown below.
The CDF of this new image is shown below.
I could say it almost fits perfectly to the desired CDF. The histogram of this new image is shown below.
As we could see, the histogram shows that it has a poor contrast which is evident in the image seen. And also, some details are not conducive for human eyes
These are all the images in the following order: original, histogram equalized, stretched histogram, desired cdf)
I also used an image from mathworks.com
I would like to thank Eduardo David for the faster way of getting the histogram and cumulative some. Also for Rafael Jaculbia for some help in the understanding of CDF. I would rate my self 10 out 10 for this activity since I have successfully transformed my image to match the CDF that we want. I want to still try many other CDF but it would take so much of time and space.
image source:http://www.mathworks.com/access/helpdesk/help/toolbox/images/index.html?/access/helpdesk/help/toolbox/images/imadjust.html





















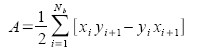
.PNG)
.PNG)
.PNG)
.PNG)
 Using the
Using the 