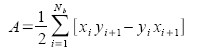
.PNG)
.PNG)
.PNG)
.PNG)
For this activity we used scilab with siptoolbox to read images we have drawn.
The dimensions of the drawn images are known.
I have drawn the following images which are shown above:
Square(side = 214 pixels)
Circle(diameter = 157 pixels)
Triangle(base = height = 214)
Rectangle(118 pixels * 158 pixels)
 Using the imread function, an image is converted to a binary matrix. Then using the follow function, the coordinates of the borders were obtained. Using the green's formula we could approximate the area of the image. Green's formula is shown above.
Using the imread function, an image is converted to a binary matrix. Then using the follow function, the coordinates of the borders were obtained. Using the green's formula we could approximate the area of the image. Green's formula is shown above.The code in scilab is shown below.
------------------------------------------------------------------------------------------------
A=imread('name of file');
[x,y]=follow(A);
x1=x;
y1=y;
x1(1)=x(size(x,'r'));
x1(2:size(x,'r'))=x(1:(size(x,'r')-1));
y1(1)=y(size(y,'r'));
y1(2:size(y,'r'))=y(1:(size(y,'r')-1));
X=x.*y1;
Y=y.*x1;
Area=0.5*(sum(X)-sum(Y))
------------------------------------------------------------------------------------------------
Calculated by Green's equation Calculated Using Dimensions %error
(pixel*pixel) (pixel*pixel)
Square 45796 45796 0
Circle 19508 19359 0.769667855
Triangle 22684.5 22898 0.932395842
Rectangle 18644 18644 0
Collaborators: Rafael Jaculbia, Eduardo David
I rate myself 10 out of 10 since I have successfully used Green's formula to estimate the area of the images and compared it to the areas calculated using the formulas for area of basic shapes. It is seen that there are no error's in square and rectangle shapes. This is because the pixels fit perfectly to the shapes since they are squares. Perfect circles, on the other hand, cannot be created through pixels. This is also true for shapes with diagonals like the triangle.
1 comment:
10 -I agree. perfect on the rectangles ha.
Post a Comment