A18 – Pattern Recognition

It fascinating for the human brain to classify objects by just seeing them even though what they see includes a lot of information such as color, size, smoothness, etc. We might not have realized it but we could classify objects almost instantaneously and make decisions based on what we see. Computers, however, takes time in order to do such things and are not perfect.

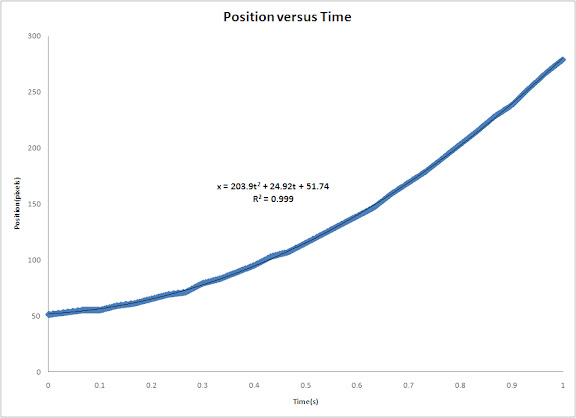
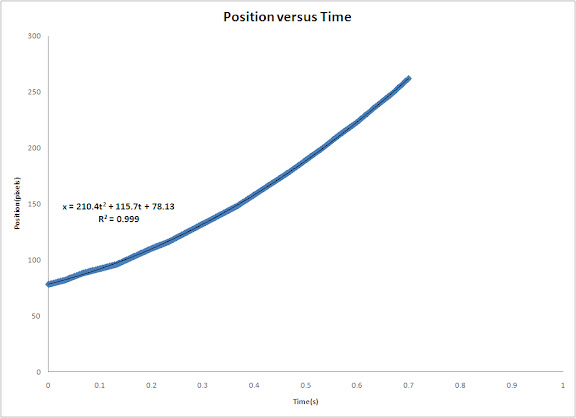
In this activity we would try to classify a set of images using the minimum distance classification.

Let wj where j = 1, 2, 3 ... W be a set of classes and W the total number of classes. If we define a representative of class wj to be its mean feature vector then

where xj is the set of ALL feature vectors in class wj and Nj is the number of samples in class wj. The simplest way of determining class membership is to classify an unknown feature vector x to the class whose mean or representative it is nearest to. For example, we can use the Euclidean distance

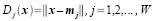
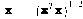
The objects I tried to sort out are the foods we bought near the math building. These are quail eggs, squid balls, chicken balls, fish balls, v-cut, piatos, and pillows. (We almost ate it while we were on the way back to CSRC.lol) We took images of each of these foods by their class then obtained their feature vector. The feature vector I used contained the mean chromaticity values r and g of the class as well as the mean of the standard deviation of its chromaticity. I believe these are the information that would most distinguish each class from one another. The images are shown below (drools....)

I tried to classify 21 samples using the minimum distance classification method and got the follow results

		Predicted
		quail eggs	squid balls	chicken balls	fish balls	piatos		v-cut		pillows
Actual	quail eggs	3
	squid balls		3
	chicken balls			3
	fish balls				3
	piatos					3
	v-cut		1			1		1
	pillows									3

The accuracy of classification is 90%. This is quite good. This means the classifiers we used are indeed the relevant information.

I give myself a grade of 10 out of 10 for this activity for having classified samples with a fairly high accuracy. I thank Raf, Jorge, Ed and Billy for helping me in this activity. Special thanks to Cole, JC and Benj for the food.^_^

A17 – Basic Video Processing

For this activity, we are tasked to apply what we learned in order to extract essential data from a video of a kinematic process. The video that I processed is that of a solid cylinder rolling along the incline (without slipping). In order to do this we decomposed the video into several images corresponding to each of its frames. We did this by using the software Virtual Dub. I used two techniques in order to get the position of the cylinder. First is image segmentation where I segmented by parametrically. Since the output is not in the range of 0-255 which is the range of grayscale values, I applied histogram stretching which I learned in the activity involving histogram manipulation. Then I applied thresholding to clear off everything except for the cylinder. The binarized video is shown below.

I plotted the position of the centroid of the cylinder versus time and then fitted a 2nd order polynomial trendline and obtained it's equation. The coefficient of the 2nd order term is just half the acceleration of the centroid since the acceleration is just the double derivative of the position with respect to time. The plot is shown below.

The acceleration using the equation of the trendline is 407.8 pixels/s^2. pixel to mm ratio is 1pixel : 1.5mm. Converting the acceleration to m/s^2, we get 0.6117 m/s^2. The code I used is shown below.

img = imread("a.jpg");
II = (img(:, :, 1) + img(:, :, 2) + img(:, :, 3));
r = img(:, :, 1)./II;
g = img(:, :, 2)./II;
b = img(:, :, 3)./II;
cen=[];
for ii=0:31
img1 = imread(string(ii)+".jpg");
I = (img1(:, :, 1) + img1(:, :, 2) + img1(:, :, 3));
R = img1(:, :, 1)./I;
G = img1(:, :, 2)./I;
B = img1(:, :, 3)./I;

//Parametric Segmentation
mnr=mean(r);
mng=mean(g);
str=stdev(r);
stg=stdev(g);
pr=1/(str*sqrt(2*%pi));
pr=pr*exp(-(R-mnr).^2/2*str);
pg=1/(stg*sqrt(2*%pi));
pg=pg*exp(-(G-mng).^2/2*stg);
P=pr.*pg;

//Histogram Stretching
imcon=[];
con=linspace(min(P),max(P),256);
for i=1:size(P,1)
for j=1:size(P,2)
dif=abs(con-P(i,j));
imcon(i,j)=find(dif==min(dif))-1;
end
end

P=imcon;
T=im2bw(P,.9);
[y,x]=find(T==max(T));
cen(ii+1)=(max(x)+min(x))/2;
imwrite(T,"new"+string(ii)+".jpg");
end

//Interpolation of position versus time
x=0:1/30:31/30;
xx=linspace(0,31/30,1000);
yy=interp1(x,cen,xx)
write("position.txt",yy');
write("time.txt",xx');


The other technique I uses was by just simply thresholding the grayscale images. I applied thresholding the grayscale images and then used a couple of closing and opening operations to remove unwanted parts. The resulting binarized video is shown below.

Again, I plotted position of the centroid of the cylinder versus time and get the trendline and equation to find the acceleration. The plot is shown below.

The acceleration using the equation of the trendline is 420.8 pixels/s^2. pixel to mm ratio is 1pixel : 1.5mm. Converting the acceleration to m/s^2, we get 0.6312 m/s^2. The code I used is shown below.

for i=0:21
im=imread(string(i)+".jpg");
im=im2bw(im,.74);
se=ones(4,10);
im=dilate(im,se);
im=erode(im,se);
se=ones(4,7);
im=erode(im,se);
im=dilate(im,se);
[y,x]=find(im==max(im));
cen(i+1)=max(x);
imwrite(im,"new"+string(i)+".jpg");
end
//Interpolation of position versus time
x=0:1/30:21/30;
xx=linspace(0,21/30,1000);
yy=interp1(x,cen,xx)
write("position.txt",yy');
write("time.txt",xx');

We need to verify if our calculated values are close to the theoretical value. I relived my Physics 101 days and solved the equation. The solution is shown in the link below (just click the pic).

The calculated theoretical acceleration is 0.6345 m/s^2. For the parametric segmentation technique the error was 3% while for the thresholding technique the error was 0.5%. Both have fairly low errors. This means that our video processing was successful.

I rate myself a 10 out of 10 (even more) for finishing this activity and showing two techniques to achieve what was required. Thank you for Raf, Ed, Jorge and Billy for helping in this activity and helping me process the video and also create a gif animation. I really enjoyed it.

A16 – Color Image Segmentation

In this activity we do image segmentation using the normalized chromaticity coordinates(NCC) of each pixel of the region of interest(ROI) of an image using their RGB values. The image and the ROI is shown above.

Since b is just 1-r-g, it is sufficient to only know the r and g values. In this way we simplify our work since we would only deal with those two values.

The first segmentation technique we used is the probability distribution estimation or the parametric segmentation. We first calculated the mean and the standard deviation of the r values of the ROI. After this, we go to the image we want to segment and then calculate the probability of each pixel having a chromaticity r to belong to the ROI by using the gaussian probability distribution given by the equation below.

We also do this for the g values with a similar equation. The joint probability is then taken as the product of p(r) and p(g) which in turn becomes our segmented image. The segmented image is shown below.

As we can see the image was segmented. The bright region is the segmented region. The darker region is the unsegmented region.

The second technique we used was histogram back projection. We first get the 2 dimensional histogram of the ROI based on its r and g values. Since both the r and g values ranges from 0 to 1 I divided it to 256 divisions which means there are 256 values in the both the r and g axis of the 2d histogram ranging from 0 to 255. The histogram is shown below.

After we get the histogram of the ROI we normalize it. For each pixel in the image we want to segment we find its r and g values and then locate it's normalized histogram value. The histogram value would now be the value of the pixel of the segmented image. The segmented image is shown below.

We see that the segmentation seems to be similar to the parametric segmentation. It is obvious that only the segment with the closest chromaticity of the ROI can be seen.

The two techniques are both good at segmenting the image. The parametric segmentation was used assuming a normal distribution but it may not always be the case. The back projection method was much faster since no further calculations of the probability distributions were needed. In this activity I think the results of the parametric segmentation was better. Using the back projection method woult make pixels which are not of the patch. equal to zero. If there were some slight variations it would not belong to be segmented anymore even if it seems to be of the same chromaticity. The parametric segmetation was based on probability so even if there were slight variations it would still be segmented as long as it is close to the chromaticity of the patch. This may explain why the parametric segmentation appears brighter and some regions are not totally dark.

I give myself a grade of 10 for this activity since I have both implemented the techniques and also seem to give a reasonable explanation of the results. Comments would be highly encourage since I want to verify if my explanations were correct.
Thank you for Ma'am Jing, Jorge, Rap, Ed and Billy for helping in this activity.