A17 – Basic Video Processing

For this activity, we are tasked to apply what we learned in order to extract essential data from a video of a kinematic process. The video that I processed is that of a solid cylinder rolling along the incline (without slipping). In order to do this we decomposed the video into several images corresponding to each of its frames. We did this by using the software Virtual Dub. I used two techniques in order to get the position of the cylinder. First is image segmentation where I segmented by parametrically. Since the output is not in the range of 0-255 which is the range of grayscale values, I applied histogram stretching which I learned in the activity involving histogram manipulation. Then I applied thresholding to clear off everything except for the cylinder. The binarized video is shown below.

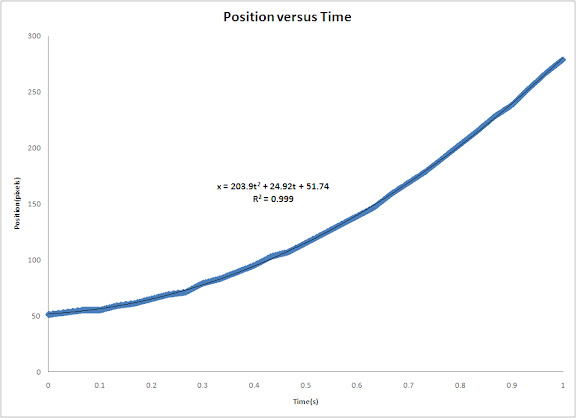
I plotted the position of the centroid of the cylinder versus time and then fitted a 2nd order polynomial trendline and obtained it's equation. The coefficient of the 2nd order term is just half the acceleration of the centroid since the acceleration is just the double derivative of the position with respect to time. The plot is shown below.

The acceleration using the equation of the trendline is 407.8 pixels/s^2. pixel to mm ratio is 1pixel : 1.5mm. Converting the acceleration to m/s^2, we get 0.6117 m/s^2. The code I used is shown below.

img = imread("a.jpg");
II = (img(:, :, 1) + img(:, :, 2) + img(:, :, 3));
r = img(:, :, 1)./II;
g = img(:, :, 2)./II;
b = img(:, :, 3)./II;
cen=[];
for ii=0:31
img1 = imread(string(ii)+".jpg");
I = (img1(:, :, 1) + img1(:, :, 2) + img1(:, :, 3));
R = img1(:, :, 1)./I;
G = img1(:, :, 2)./I;
B = img1(:, :, 3)./I;

//Parametric Segmentation
mnr=mean(r);
mng=mean(g);
str=stdev(r);
stg=stdev(g);
pr=1/(str*sqrt(2*%pi));
pr=pr*exp(-(R-mnr).^2/2*str);
pg=1/(stg*sqrt(2*%pi));
pg=pg*exp(-(G-mng).^2/2*stg);
P=pr.*pg;

//Histogram Stretching
imcon=[];
con=linspace(min(P),max(P),256);
for i=1:size(P,1)
for j=1:size(P,2)
dif=abs(con-P(i,j));
imcon(i,j)=find(dif==min(dif))-1;
end
end

P=imcon;
T=im2bw(P,.9);
[y,x]=find(T==max(T));
cen(ii+1)=(max(x)+min(x))/2;
imwrite(T,"new"+string(ii)+".jpg");
end

//Interpolation of position versus time
x=0:1/30:31/30;
xx=linspace(0,31/30,1000);
yy=interp1(x,cen,xx)
write("position.txt",yy');
write("time.txt",xx');


The other technique I uses was by just simply thresholding the grayscale images. I applied thresholding the grayscale images and then used a couple of closing and opening operations to remove unwanted parts. The resulting binarized video is shown below.

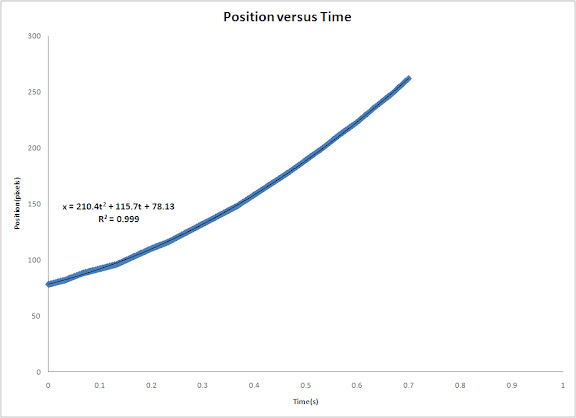
Again, I plotted position of the centroid of the cylinder versus time and get the trendline and equation to find the acceleration. The plot is shown below.

The acceleration using the equation of the trendline is 420.8 pixels/s^2. pixel to mm ratio is 1pixel : 1.5mm. Converting the acceleration to m/s^2, we get 0.6312 m/s^2. The code I used is shown below.

for i=0:21
im=imread(string(i)+".jpg");
im=im2bw(im,.74);
se=ones(4,10);
im=dilate(im,se);
im=erode(im,se);
se=ones(4,7);
im=erode(im,se);
im=dilate(im,se);
[y,x]=find(im==max(im));
cen(i+1)=max(x);
imwrite(im,"new"+string(i)+".jpg");
end
//Interpolation of position versus time
x=0:1/30:21/30;
xx=linspace(0,21/30,1000);
yy=interp1(x,cen,xx)
write("position.txt",yy');
write("time.txt",xx');

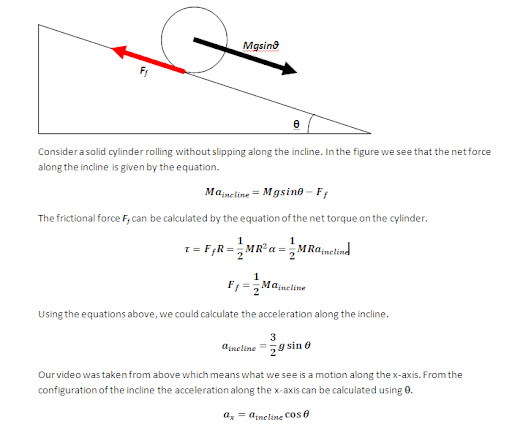
We need to verify if our calculated values are close to the theoretical value. I relived my Physics 101 days and solved the equation. The solution is shown in the link below (just click the pic).

The calculated theoretical acceleration is 0.6345 m/s^2. For the parametric segmentation technique the error was 3% while for the thresholding technique the error was 0.5%. Both have fairly low errors. This means that our video processing was successful.

I rate myself a 10 out of 10 (even more) for finishing this activity and showing two techniques to achieve what was required. Thank you for Raf, Ed, Jorge and Billy for helping in this activity and helping me process the video and also create a gif animation. I really enjoyed it.