In mathematics, the discrete Fourier transform (DFT) is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function (which is often a function in the time domain). But the DFT requires an input function that is discrete and whose non-zero values have a limited (finite) duration.
Discrete Fourier Transfor (DFT) is on of the specific forms of Fourier analysis. Basically one function is transformed into its frequency domain of the original function. The DFT requires an input function that is discrete and whose non-zero values have a finite duration.
Source:http://en.wikipedia.org/wiki/Discrete_Fourier_transform
The sequence of N ci x0, ..., xN−1 is transformed into the sequence of N complex numbers X0, ..., XN−1 by the DFT according to the formula:
Discrete Fourier Transfor (DFT) is on of the specific forms of Fourier analysis. Basically one function is transformed into its frequency domain of the original function. The DFT requires an input function that is discrete and whose non-zero values have a finite duration.
Source:http://en.wikipedia.org/wiki/Discrete_Fourier_transform
The sequence of N ci x0, ..., xN−1 is transformed into the sequence of N complex numbers X0, ..., XN−1 by the DFT according to the formula:
For a square image of size N×N, the two-dimensional DFT is given by:
To obtain the result for the above equations, a double sum has to be calculated for each image point. However, because the Fourier Transform is separable, it can be written as
where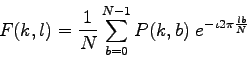
To obtain the result for the above equations, a double sum has to be calculated for each image point. However, because the Fourier Transform is separable, it can be written as
where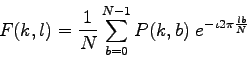
Source:http://homepages.inf.ed.ac.uk/rbf/HIPR2/fourier.htm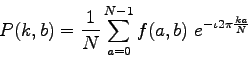
This means that we could first get the Fourier transform of the image along the columns(rows) to get P(k,b) then get the Fourier transform of P(k,b) along the rows(columns) to get the 2-dimensional Fourier transform.
a) Light from a fluorescent lamp is known to flicker at 120Hz. What should be the threshold sampling interval for accurate FT analysis?
From the Nyquist Theorem, the sampling interval Δt tells us the maximum
frequency Fmax the FT transform can detect without aliasing and it is given by
Fmax=(2Δt)^-1
In this case our Fmax=120Hz
Δt=(2Fmax)^-1=(240Hz)^-1=0.0041667 s
b) What is the effect of increasing the number of samples N in the FT?
Increasing the number of samples N would result to an increase in the sampling interval T and an increase in resolution because Δf is decreased. The first image is the FFT with N=256 and the second is with N=1000. We could see that the one with higher N has a sharper graph which means that the resolution is better.


c) What is the effect of decreasing the sampling interval Δt in the FT?
It would increase Fmax meaning it could detect more frequencies. But the resolution is sacrificed because Δf is also increased. This can be seen below. The first has Δt=2/256 and the second is Δt=2/1000.


d) What is the effect of fixing the total time interval T but increasing the
number of samples N?
Increasing the number of samples N fixing the time interval T would result to an increase in Fmax which means it could now detect more frequencies. But it would have the same resolution. This seen below. The first has N=256 and the second has N=1000.


Collaborators: Rafael Jaculbia
I rate myself 10 out of 10 since I have successfully finished the task and have also verified my answers using simulations in scilab.
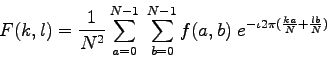
No comments:
Post a Comment